Search Results
Results for: 'Introduction to Public Health video'

This video is a supplement for students who are reading "Introduction To The Theory Of Computation" by Michael Sipser. I took the liberty of using the terminology from the textbook.

CS125 - Formal Definition of DFA
This video is a supplement for students who are reading "Introduction To The Theory Of Computation" by Michael Sipser. I took the liberty of using the terminology from the textbook.

CS125 - Regular Languages Closed under Complement
This video is a supplement for students who are reading "Introduction To The Theory Of Computation" by Michael Sipser. I took the liberty of using the terminology from the textbook.

CS125 - Regular Languages Closed under Intersection and Union
This video is a supplement for students who are reading "Introduction To The Theory Of Computation" by Michael Sipser. I took the liberty of using the terminology from the textbook.

This video includes a definition of bio-conversions, discussion of the Cell Theory of Life as well as the difference between Eukaryotes, Prokaryotes as well as quick mention of Prions.

CS125 - Formal Definition of NFA
This video is a supplement for students who are reading "Introduction To The Theory Of Computation" by Michael Sipser. I took the liberty of using the terminology from the textbook.

Introduction to Carbohydrates Through Disaccharides
This video includes a discussion of CHO's in general through a discussion of mono and di saccharides
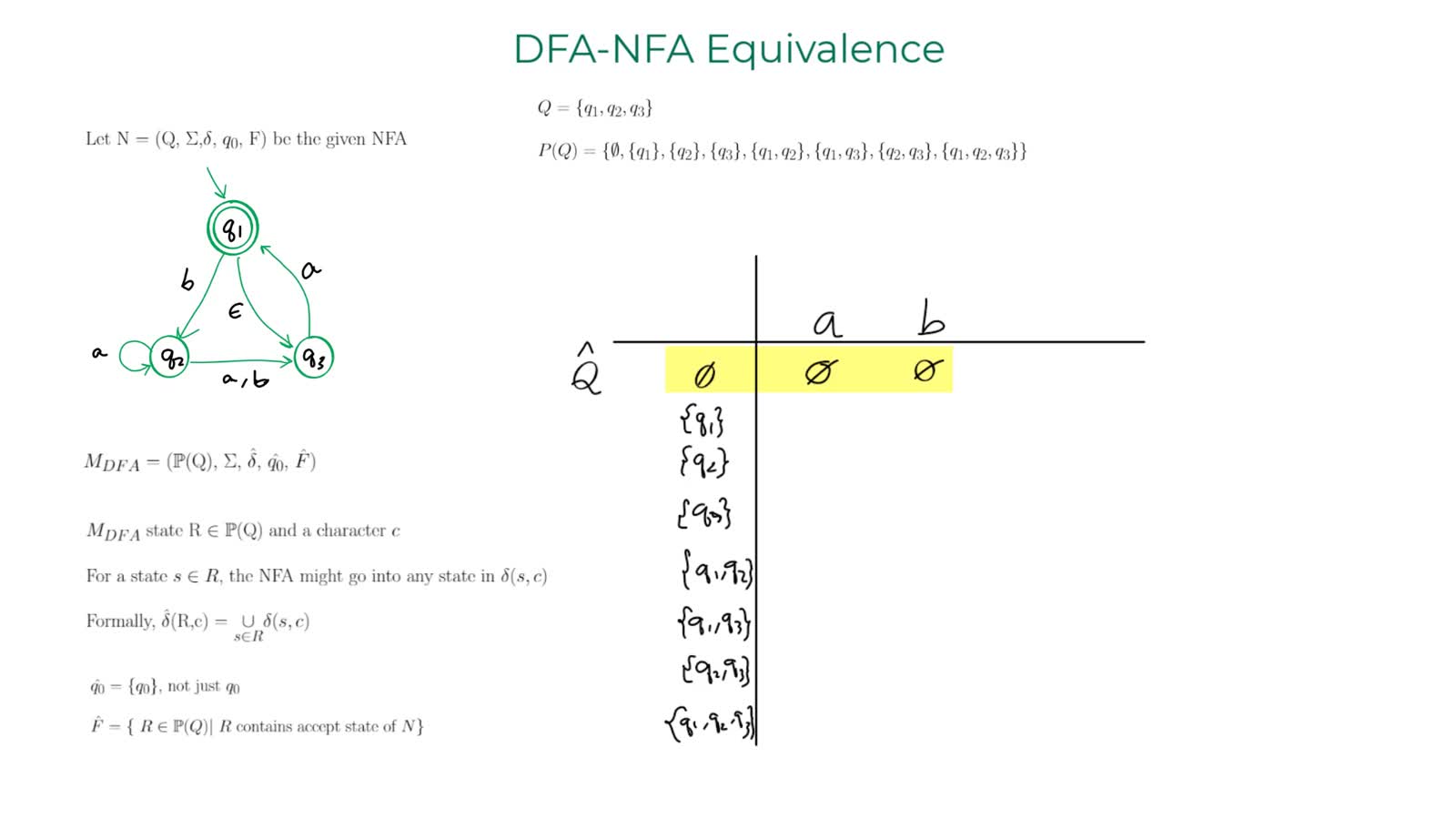
This video is a supplement for students who are reading "Introduction To The Theory Of Computation" by Michael Sipser. I took the liberty of using the terminology from the textbook.

Introduction to proofs PHIL 013AB
A video on what proofs are, which explains the concept of simple derivation, and how to do proofs with one proof rule, Modus Ponens.